Bayes_Poisson のバックアップ(No.6)

バックアップ一覧
差分を表示
現在との差分を表示
ソースを表示
Bayes_Poisson へ行く。
- 1 (2008-09-18 (木) 11:20:50)
- 2 (2008-09-18 (木) 14:13:35)
- 3 (2008-09-18 (木) 17:20:23)
- 4 (2008-09-18 (木) 18:21:38)
- 5 (2008-09-19 (金) 08:36:24)
- 6 (2008-09-19 (金) 17:43:23)

Rの備忘録

授業で使います．

ポアソンの共役事前分布はガンマ分布とする
R での実行例
予測分布と負の二項分布
ポアソン回帰
参考文献

_ ポアソンの共役事前分布はガンマ分布とする

Gelman et al.: Bayesian Data Analysis, p.52, 2nd Edition．

ポアソン分布とガンマ分布の関係については繁桝算男『ベイズ統計入門』64ページを参照．

ポアソン分布
#mimetex(p(y|\theta) = \frac{\theta^y \, e^{-\theta}}{y!})
尤度
#mimetex(\bf{y} = y_i, \dots , y_n)

#mimetex(p(\bf{y}|\theta) = l(\theta|\bf{y}) = \Pi \frac{1}{y_i!} \theta^{y_i} \, e^{-\theta})

#mimetex( \propto \theta^{t(y)} \, e^{-n \theta}) 指数属で表現すると

#mimetex( \propto e^{-n\theta}\, e^{t(y) log \theta} ) 文系学生相手にするので，指数法則を指摘する．

#mimetex(\theta^y = e^{log(\theta^y)} = e^{y log \theta}) 指数属とは関数が次の形で表されること(Lee: Bayesian Statistics, pp.60)．

#mimetex(p(\bf{x}| \theta) = g(\bf{x}) \, h(\theta) \, e^{t(\bf{x}) \, \phi(\theta)}) 上の式では&mimetex(\frac{1}{y!});が消えているので注意
自然共役事前分布
#mimetex(p(\theta) \propto (e^{-\theta})^n e^{v log \theta} )
事後分布
#mimetex(\theta|\bf{y} \sim Gamma(\alpha + n \bar{y}, \beta + n))
医学関係ではポアソン分布を次のように書いている．
#mimetex(y_i \sim Poisson(x_i \theta)) &mimetex(y_i); と &mimetex(x_i); が観測数で，&mimetex(\theta); が未知のパラメータだが，&mimetex(x); を exposure，&mimetex(\theta); をrate と表現しており，分野違いの人間はいつまでたっても馴染みにくい．

↑

_ R での実行例

Albert Bayesian: Computation with R より
- 米国のある病院での心臓手術が失敗するケース数&mimetex(y); を考える．ここで失敗とは手術後30以内に死亡することである．これはポアソン分布に従うとする．手術(exposure)の総数を&mimetex(e);，exposureあたりの死亡率を&mimetex(\lambda); とすると，
- 米国のある病院での心臓手術が失敗するケース数&mimetex(y); を考える．ここで失敗とは手術後30以内に死亡することである．これはポアソン分布に従うとする．手術(exposure)の総数を&mimetex(e);，exposureあたりの死亡率を&mimetex(\lambda); とすると，
  #mimetex(y \sim Poisson(e \lambda))
- &mimetex(\lambda);の最尤推定量は &mimetex( \bar{\lambda} = y/e);である．
- 上で述べたように事前共役分布はガンマ分布だが，二つのパラメータを設定する必要がある．ここでは，いま対象としている病院と同じ手術レベルの他の病院のデータを参考にして，&mimetex(\alpha = 16); と&mimetex(\beta = 15174); とする．すなわち事前分布は
  #mimetex(\theta^{16-1} \, e^{-15174\, \theta} = Gamma(16,15174 ))
- すると事後分布は &mimetex(16 + y, 15174 + e); のガンマ分布となる．

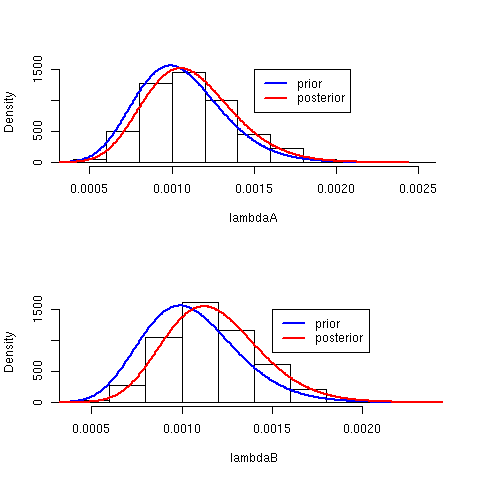
さて，ここで新たに手術例が66件で，うち失敗が1件の病院と，手術例が1767件で，うち失敗が4件の病院があるとする．

my.alpha <- 16
my.beta <- 15174
lam <- my.alpha/my.beta
lambdaA <- rgamma(1000, shape = my.alpha + 1, rate = my.beta + 66)
lambdaB <- rgamma(1000, shape = my.alpha + 1767, rate = my.beta + 4)
lambda <- seq(0, max(c(lambdaA, lambdaB)), length = 500)

par(mfrow = c(2,1))# , mar = rep(1, 4))
hist(lambdaA, freq = FALSE, main = "", ylim =c(0, 1600))
lines(lambda, dgamma(lambda, shape = my.alpha, my.beta),
           col = "blue", lwd = 3)
lines(lambda, dgamma(lambda, shape = my.alpha+ 1, 
           my.beta + 66),  col = "red", lwd = 3)
legend(0.0015, 1500, legend= c("prior", "posterior"), 
           col =  c("blue","red"), lwd = 3)
hist(lambdaB, freq = FALSE, main = "", ylim =c(0, 1600))
lines(lambda, dgamma(lambda, shape = my.alpha, my.beta),
           col = "blue", lwd = 3)
lines(lambda, dgamma(lambda, shape = my.alpha+ 4, 
           my.beta + 1767),  col = "red", lwd = 3)
legend(0.0015, 1500, legend= c("prior", "posterior"), 
           col =   c("blue","red"), lwd = 3)

↑

_ 予測分布と負の二項分布

（事前）予測密度関数&mimetex(f(x)); は，&mimetex(f(y|\lambda)); をサンプルのポアソン分布，&mimetex(g(\lambda)); を事前分布，&mimetex(g(y|\lambda)); を事後分布とすると，
#mimetex(f(y) = \frac{f(y|\lambda) \, g(\lambda)}{g(y|\lambda)})

#mimetex(p(y) = \frac{Poisson(y|\theta) Gamma(\theta|\alpha, \beta)}{Gamma(\theta|\alpha+y, 1 + \beta)})

#mimetex(=\frac{\Gamma (\alpha + y) \beta^\alpha}{\Gamma(\alpha)y! \, (1+\beta)^{\alpha+y}})

#mimetex(y \sim Neg-bin(\alpha, \beta)) これはポアソン分布の&mimetex(\theta); がガンマ分布に従う混合分布である．

↑

_ ポアソン回帰

豊田秀樹『マルコフ連鎖モンテカルロ法』は良い本なんだけど，掲載サンプルではBRugsパッケージの利用を前提としている．ところがBRugsはCRANのパッケージから外されている．ポアソン回帰ならば，MCMCpackでも間に合う．以下，『マルコフ連鎖モンテカルロ法』p.107掲載データ（生化学専攻大学院生の論文執筆数を性別，既婚・独身，子供の数で説明する）を glm と MCMCpoisson で実行する．データMCMCpoisson.Rを読み込んで

library(MCMCpack)
source("MCMCpoisson.R")
posterior <- MCMCpoisson(y ~ x1 + x2 + x3)
plot(posterior)
summary(posterior)
Iterations = 1001:11000
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 10000 
1. Empirical mean and standard deviation for each variable,
  plus standard error of the mean:
              Mean      SD  Naive SE Time-series SE
(Intercept)  0.6389 0.05432 0.0005432       0.002321
x1          -0.2852 0.05355 0.0005355       0.002204
x2           0.1300 0.06095 0.0006095       0.002382
x3          -0.1623 0.03891 0.0003891       0.001549
2. Quantiles for each variable:
              2.5%      25%     50%     75%    97.5%
(Intercept)  0.5323  0.60324  0.6397  0.6746  0.74692
x1          -0.3908 -0.32266 -0.2837 -0.2498 -0.18105
x2           0.0082  0.09005  0.1311  0.1703  0.25447
x3          -0.2396 -0.18926 -0.1622 -0.1360 -0.08486

一般線形化モデル

pois.glm <- glm(y ~ x1 + x2 + x3,family=poisson())
summary(pois.glm)
Call:
glm(formula = y ~ x1 + x2 + x3, family = poisson())
Deviance Residuals: 
   Min       1Q   Median       3Q      Max  
-2.0776  -1.6856  -0.3729   0.4936   6.9981  
Coefficients:
           Estimate Std. Error z value Pr(>|z|)    
(Intercept)  0.63656    0.05457  11.665  < 2e-16 ***
x1          -0.28549    0.05433  -5.255 1.48e-07 ***
x2           0.13271    0.06092   2.179   0.0294 *  
x3          -0.16118    0.03934  -4.097 4.19e-05 ***
(Dispersion parameter for poisson family taken to be 1)
   Null deviance: 1817.4  on 914  degrees of freedom
Residual deviance: 1776.7  on 911  degrees of freedom
AIC: 3452.5

Number of Fisher Scoring iterations: 5

↑

_ 参考文献

Gelman et al.: Bayesian Data Analysis, 2nd Edition,Chapman

Lee: Bayesian Statistics, Hodder Arnold

Albert Bayesian: Computation with R, Springer

繁桝算男『ベイズ統計入門』東京大学

豊田秀樹『マルコフ連鎖モンテカルロ法』朝倉書店

こういうページも参考に．

アールメカブ