Bayes_Poisson のバックアップ(No.4)
- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- Bayes_Poisson へ行く。
授業で使います.
_ ポアソンの共役事前分布はガンマ分布とする
(Gelman et al.: Bayesian Data Analysis, p.52, 2nd Edition).
- ポアソン分布
#mimetex(p(y|\theta) = \frac{\theta^y \, e^{-\theta}}{y!})
- 尤度
#mimetex(\bf{y} = y_i, \dots , y_n)
#mimetex(p(\bf{y}|\theta) = l(\theta|\bf{y}) = \Pi \frac{1}{y_i!} \theta^{y_i} \, e^{-\theta})
#mimetex( \propto \theta^{t(y)} \, e^{-n \theta}) 指数属で表現すると
#mimetex( \propto e^{-n\theta}\, e^{t(y) log \theta} ) 文系学生相手にするので,指数法則を指摘する.
#mimetex(\theta^y = e^{log(\theta^y)} = e^{y log \theta}) 指数属とは関数が次の形で表されること(Lee: Bayesian Statistics, pp.60).
#mimetex(p(\bf{x}| \theta) = g(\bf{x}) \, h(\theta) \, e^{t(\bf{x}) \, \phi(\theta)}) 上の式では&mimetex(\frac{1}{y!});が消えているので注意
- 自然共役事前分布
#mimetex(p(\theta) \propto (e^{-\theta})^n e^{v log \theta} )
- 事後分布
#mimetex(\theta|\bf{y} \sim Gamma(\alpha + n \bar{y}, \beta + n))
- 医学関係ではポアソン分布を次のように書いている.
#mimetex(y_i \sim Poisson(x_i \theta)) &mimetex(y_i); と &mimetex(x_i); が観測数で,&mimetex(\theta); が未知のパラメータだが,&mimetex(x); を exposure,&mimetex(\theta); をrate と表現しており,分野違いの人間はいつまでたっても馴染みにくい.
_ R での実行例
- Albert Bayesian: Computation with R より
- 米国のある病院での心臓手術が失敗するケース数&mimetex(y); を考える.ここで失敗とは手術後30以内に死亡することである.これはポアソン分布に従うとする.手術(exposure)の総数を&mimetex(e);,exposureあたりの死亡率を&mimetex(\lambda); とすると,
- 米国のある病院での心臓手術が失敗するケース数&mimetex(y); を考える.ここで失敗とは手術後30以内に死亡することである.これはポアソン分布に従うとする.手術(exposure)の総数を&mimetex(e);,exposureあたりの死亡率を&mimetex(\lambda); とすると,
#mimetex(y \sim Poisson(e \lambda))
- &mimetex(\lambda);の最尤推定量は &mimetex( \bar{\lambda} = y/e);である.
- 上で述べたように事前共役分布はガンマ分布だが,二つのパラメータを設定する必要がある.ここでは,いま対象としている病院と同じ手術レベルの他の病院のデータを参考にして,&mimetex(\alpha = 16); と&mimetex(\beta = 15174); とする.すなわち事前分布は
#mimetex(\theta^{16-1} \, e^{-15174\, \theta} = Gamma(16,15174 ))
- すると事後分布は &mimetex(16 + y, 15174 + e); のガンマ分布となる.
- さて,ここで新たに手術例が66件で,うち失敗が1件の病院と,手術例が1767件で,うち失敗が4件の病院があるとする.
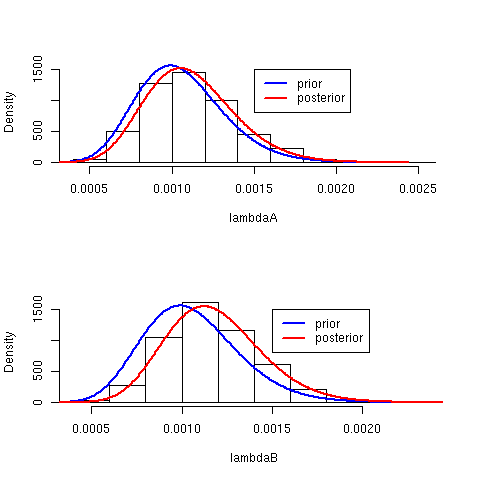
my.alpha <- 16 my.beta <- 15174 lam <- my.alpha/my.beta lambdaA <- rgamma(1000, shape = my.alpha + 1, rate = my.beta + 66) lambdaB <- rgamma(1000, shape = my.alpha + 1767, rate = my.beta + 4) lambda <- seq(0, max(c(lambdaA, lambdaB)), length = 500)
par(mfrow = c(2,1))# , mar = rep(1, 4))
hist(lambdaA, freq = FALSE, main = "", ylim =c(0, 1600))
lines(lambda, dgamma(lambda, shape = my.alpha, my.beta),
col = "blue", lwd = 3)
lines(lambda, dgamma(lambda, shape = my.alpha+ 1,
my.beta + 66), col = "red", lwd = 3)
legend(0.0015, 1500, legend= c("prior", "posterior"),
col = c("blue","red"), lwd = 3)
hist(lambdaB, freq = FALSE, main = "", ylim =c(0, 1600))
lines(lambda, dgamma(lambda, shape = my.alpha, my.beta),
col = "blue", lwd = 3)
lines(lambda, dgamma(lambda, shape = my.alpha+ 4,
my.beta + 1767), col = "red", lwd = 3)
legend(0.0015, 1500, legend= c("prior", "posterior"),
col = c("blue","red"), lwd = 3)
_ 予測分布は負の二項分布となる.
- (事前)予測密度関数&mimetex(f(x)); は,&mimetex(f(y|\lambda)); をサンプルのポアソン分布,&mimetex(g(\lambda)); を事前分布,&mimetex(g(y|\lambda)); を事後分布とすると,
#mimetex(f(y) = \frac{f(y|\lambda) \, g(\lambda)}{g(y|\lambda)}) こういうページも参考に.