第2章 データ分析の王道?
最終更新日 2013 09 14
- バラツキ ーー その1(分散)
- 分散 と標準偏差
平均値を中心にデータがどれだけバラついているかを表すのが分散と標準偏差です.
例:ある試験の得点データを用意
> siken <- c(50, 60, 70, 50, 70, 80, 60, 80, 70,60,50,90,40) > siken [1] 50 60 70 50 70 80 60 80 70 60 50 90 40
例:分散を式通りに計算してみます.まず全体平均をそれぞれから引きます.
> siken - mean (siken) [1] -13.846154 -3.846154 6.153846 -13.846154 6.153846 [6] 16.153846 -3.846154 16.153846 6.153846 -3.846154 [11] -13.846154 26.153846 -23.846154例:上の式に自乗する計算を追加します.
> (siken - mean (siken))^2 [1] 191.71598 14.79290 37.86982 191.71598 37.86982 [6] 260.94675 14.79290 260.94675 37.86982 14.79290 [11] 191.71598 684.02367 568.63905
例:それぞれ自乗した値を合計します.「平方和 」を取るといいます.
> sum ((siken - mean (siken))^2) [1] 2507.692
例:平方和をデータ数で割る.データ数は length() 関数を使って求めることができます.
> sum ((siken - mean (siken))^2) / length (siken) [1] 192.8994
例:この結果全体から平方根を求めれば,それが標準偏差です.sqrt()関数を使います.
> sqrt (sum ((siken - mean (siken))^2) / length (siken)) [1] 13.88882
- バラツキ ーー その2(不偏分散)
- 不偏分散とその標準偏差
ただし,あとがきで述べた不偏分散を求めるのであれば,もっと簡単です.var()関数(variance=分散)やsd()関数(standard devation=標準偏差)を使います.
不偏分散は平方和を,データ数マイナス1で割った数値です.
例:sikenデータの平均と分散,標準偏差を確認
> # 平均 > mean (siken) [1] 63.84615 > # 不偏分散 > var (siken) [1] 208.9744 > # 不偏分散にもとづく標準偏差 > sd (siken) [1] 14.45595
- 確率分布
- データ分析(統計学)では確率分布という言葉がたくさん出てきます.
確率分布は,ある事柄がある条件で生じる可能性を数学的に表現したものです.
もちろん現実のデータと理論的な確率分布が完全に一致するわけではありません.
それでも,確率分布を応用することで,現実のデータを検討する手がかりになります.
- 正規分布
もっとも有名な確率分布です.身長体重,学校の成績など,現実の多くのデータを確率的に説明するのに使われる分布です.
下の図のような曲線になるのが特徴です.
> curve (dnorm, from = -4, to = 4)
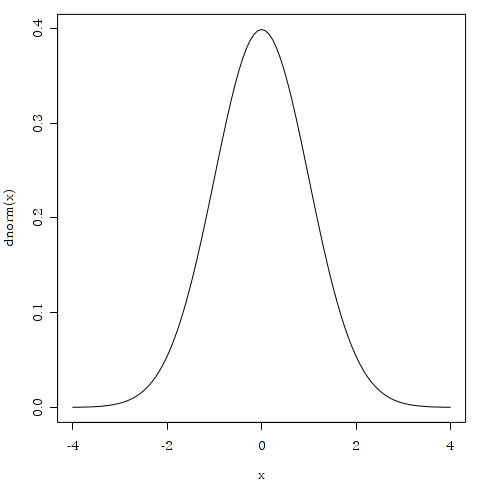
これは平均が0で標準偏差が1の正規分布がえがく曲線です.曲線の下の面積が 1 (100%) となります. curve()という曲線をえがく関数に,正規分布を意味する dnorm を指定し,X軸が -4 から +4 の範囲の曲線を描いています.
- ヒストグラム
ヒストグラムは,データを区間ごとに分割して,それぞれ区間の属するデータの数をY軸にとったグラフです.X軸は,区間を表します.
結果として,棒グラフが並んだグラフとなります.このとき,中央の棒が大きく,左右対象に棒が低くなっている場合,データを正規分布にあてはめて考えることができます.
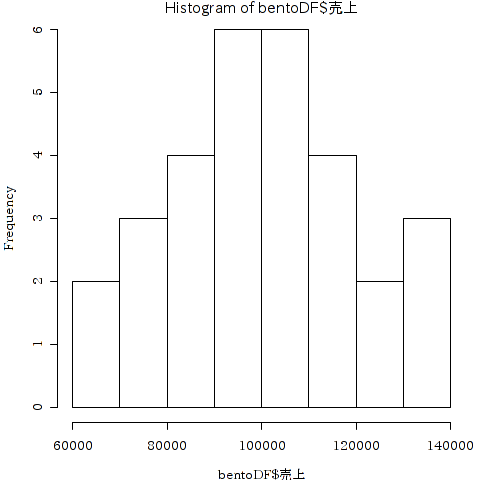
ここで,正規屋さんの一ヶ月の売上をヒストグラムにしてみます.ヒストグラムにしたとき,正規分布の曲線におおむね一致しているようなら,確率分布として正規分布を想定して分析を行うことができます.
> hist (bentoDF$売上)
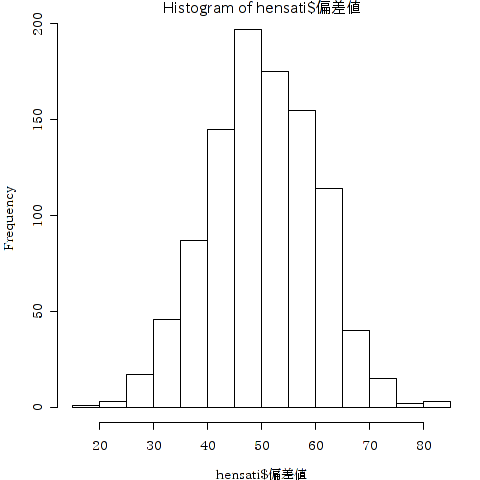
例:偏差値データのヒストグラムです.偏差値は平均が 50,標準偏差が 10と設定されています.
> hist(hensati$偏差値)
- 二項分布
「産婦人科で昨日生まれた新生児にしめる女児の人数」とか 「友達10名のうち,サザエさんを観た人数」とかを検討するのに使われる確率分布です.
例:10枚のコインを投げて表が出る枚数それぞれの確率をグラフにしてみます.plot()関数は3章で扱いますが,「type="h"」 という指定は,ヒストグラム風に描くことを意味しています.
> plot(確率 ~ 枚数 , type = "h", data = coin)
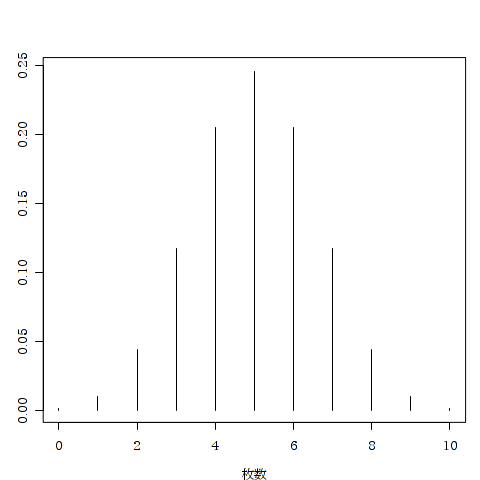
正規分布の場合とは異なり,面積ではなく,それぞれの棒の高さ(Y軸の目盛り)そのものが確率に対応しています.
この棒の数が増えると正規分布の形状に近づいていきます.
コインを30枚なげて,表が出る枚数(0枚から30枚)の確率と,コインを100枚投げて表が出る枚数の確率をそれぞれ求めたうえでヒストグラムにしてみます.
> coin30 <- dbinom(0:30, 30, 0.5) > coin100 <- dbinom(0:100, 100, 0.5) > par(mfrow = c(1,2)) > plot (0:30, coin30, type = "h", main = "コイン30枚の場合") > plot (0:100, coin100, type = "h" , main = "コイン100枚の場合")
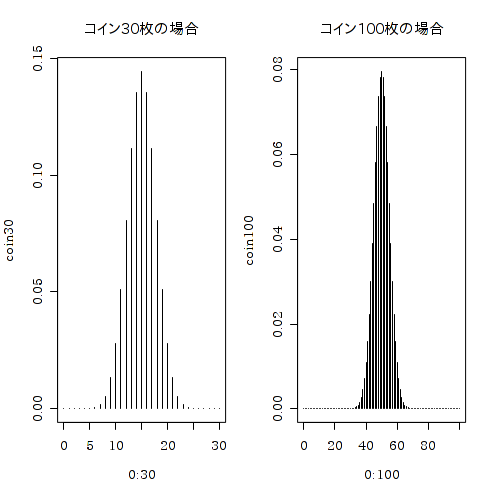
dbinom関数は二項分布の確率を計算します.引数 0:30 は0から30までを表し,次の30は,30枚投げることを意味します.最後の0.5は,1枚のコインで表が出る確率です.0.5(50%) と指定しています.
「par(mfrow = c(1,2))」は1枚のグラフを1行2列に分割する命令です.
