第3章 相関と回帰
最終更新日 2013 09 14
- 散布図
- ビールデータ(beer)は気温と消費量などの変数を列とするデータフレームからです.
例:head()関数を使って冒頭だけ表示します.
> head (beer) 月 気温 消費量 ミリ 消費量の予測 1 1 5.5 2.38 2380 3.36 2 2 6.6 3.85 3850 3.57 3 3 8.1 4.41 4410 3.85 4 4 15.8 5.67 5670 5.32 5 5 19.5 5.44 5440 6.03 6 6 22.4 6.03 6030 6.58
ここから「気温」と「消費量」という2つの変数について,互いの関係を散布図で描いてみますす.
> plot (消費量 ~ 気温, data = beer)
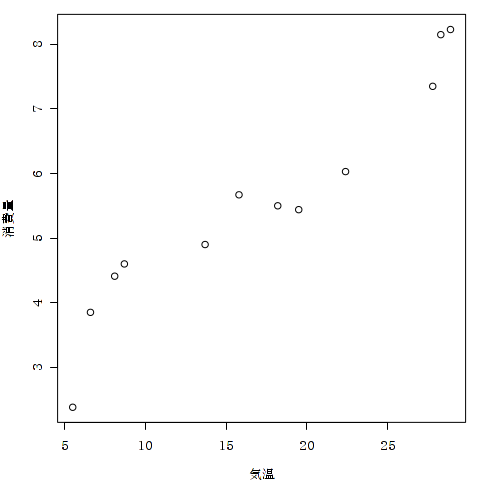
「消費量 ~ 気温」は消費量をY軸に,気温をX軸にとる,という命令です.
- 地価データ(tika)
これは「距離」と「地価」の2列からなります
例:head()関数を使って冒頭だけ表示します
> head (tika) 距離 地価 1 1178.7 336.7 2 1122.4 365.7 3 1070.1 372.0 4 1049.8 377.7 5 1040.1 388.5 6 1036.0 403.5
地価と駅からの距離の関係について散布図を作成してみます.
> plot (地価 ~ 距離, data = tika)
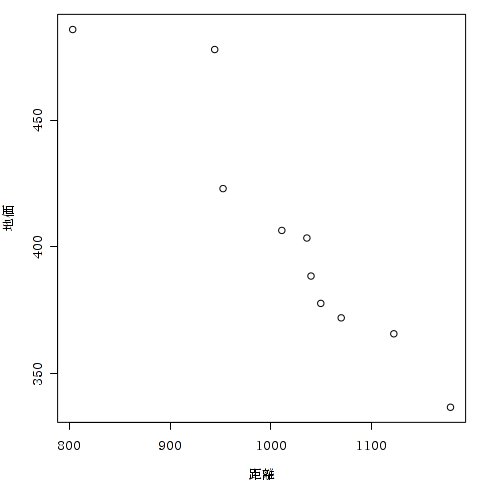
「地価 ~ 距離」は地価をY軸に,距離をX軸にとる,という命令です - アニメデータ(anime)
これは「アニメ(視聴時間)」と「(勉強)時間」の2列からなります.
例:head()関数を使って冒頭だけ表示します
> head (anime)
アニメ視聴時間と勉強時間の関係について散布図を作成してみます.
> plot (アニメ ~ 時間, data = tika) アニメ 勉強時間 1 5.585529 2.883752 2 5.709466 4.817312 3 4.890697 3.370628 4 4.546503 3.520216 5 5.605887 2.249468 6 3.182044 3.816900
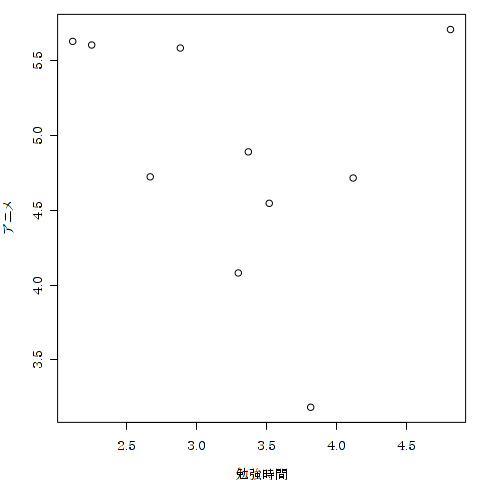
「アニメ ~ 時間」はアニメ視聴時間をY軸に,距離をX軸にとる,という命令です.
- データ操作
- ビールデータ(beer)
消費量(変数)だけにアクセスする方法があります.
「$」記号を使います.
> beer $ 消費量 [1] 2.38 3.85 4.41 5.67 5.44 6.03 8.15 8.23 7.35 5.50 4.90 4.60
- 偏差
偏差とは,全体平均を個々のデータから引いた値です. それぞれの変数の偏差を求めます.
> beer$消費量 - mean (beer$消費量) [1] -3.1625 -1.6925 -1.1325 0.1275 -0.1025 0.4875 2.6075 [8] 2.6875 1.8075 -0.0425 -0.6425 -0.9425 > beer$気温 - mean (beer$気温) [1] -11.458333 -10.358333 -8.858333 -1.158333 2.541667 [6] 5.441667 11.341667 11.941667 10.841667 1.241667 [11] -3.258333 -8.258333 - 偏差どうしを掛け算
それぞれの偏差を掛けます.
> (beer$消費量 - mean (beer$消費量)) * ( beer$気温 - mean (beer$気温)) [1] 36.23697917 17.53147917 10.03206250 -0.14768750 [5] -0.26052083 2.65281250 29.57339583 32.09322917 [9] 19.59631250 -0.05277083 2.09347917 7.78347917 > (beer$ミリ - mean (beer$ミリ)) * ( beer$気温 - mean (beer$気温)) [1] 36236.97917 17531.47917 10032.06250 -147.68750 [5] -260.52083 2652.81250 29573.39583 32093.22917 [9] 19596.31250 -52.77083 2093.47917 7783.47917 - 偏差平方和
それぞれの合計です.
> sum ((beer$消費量 - mean (beer$消費量)) * (beer$気温 - mean(beer$気温))) [1] 157.1322 > sum ((beer$ミリ - mean (beer$ミリ)) * (beer$気温 - mean (beer$気温))) [1] 157132.2 - 共分散
それぞれの共分散です.
> sum ( (beer$消費量 - mean (beer$消費量)) * ( beer$気温 - mean (beer$気温)) ) / 12 [1] 13.09435 > sum ( (beer$ミリ - mean (beer$ミリ)) * ( beer$気温 - mean (beer$気温)) ) / 12 [1] 13094.35 - 標準偏差
それぞれの標準偏差です.
> sqrt (sum ( (beer$消費量 - mean (beer$消費量))^2) / 12) [1] 1.658429 > sqrt (sum ( (beer$ミリ - mean (beer$ミリ))^2) / 12) [1] 1658.429 > sqrt (sum ( (beer$気温 - mean (beer$気温))^2) / 12) [1] 8.28457 - 相関係数
以上の計算結果を使うと,相関係数を計算できます.端数の処理の関係で,小数点以下が一致していませんが,正確に計算すれば一致します.
> 13.1 / ( 1.66 * 8.28) [1] 0.9530877 > 13094 / (1658.43 * 8.28) [1] 0.953553 - cor()関数で求める相関係数
とはいえ,実は相関係数を簡単に計算してくれる関数があります!cor()関数に,2つの変数名をカンマで挟んで指定します.
> cor (beer$消費量 , beer$気温) [1] 0.9530536 > cor (beer$ミリ , beer$気温) [1] 0.9530536
- cov()関数による共分散
また共分散をまとめて計算してくれる関数 cov() も,実はあります.
> cov (beer$消費量, beer$気温) [1] 14.28475 > cov (beer$ミリ, beer$気温) [1] 14284.75
ただし分母をデータ数ではなく,データ数マイナス1にした不偏分散ですので,上の計算結果とは一致しません.
14.28475 * 11 / 12 を実行すれば,上の計算結果に一致します.
- 正規化
本書で理論的な計算式を示しましたが,実はscale() 関数を使って求めることもできます.
> (dat1 <- c(1, 2, 3, 4, 5)) [1] 1 2 3 4 5 > (dat1000 <- dat1 * 1000) [1] 1000 2000 3000 4000 5000 > scale(dat1) [,1] [1,] -1.2649111 [2,] -0.6324555 [3,] 0.0000000 [4,] 0.6324555 [5,] 1.2649111 attr(,"scaled:center") [1] 3 attr(,"scaled:scale") [1] 1.581139 > scale(dat1000) [,1] [1,] -1.2649111 [2,] -0.6324555 [3,] 0.0000000 [4,] 0.6324555 [5,] 1.2649111 attr(,"scaled:center") [1] 3000 attr(,"scaled:scale") [1] 1581.139
- 回帰分析
- 回帰分析はlm()関数で実行します.
使い方は
lm ( 目的変数名 〜 説明変数名, data = データ名)
となります.
チルダ記号(〜)を挟んで変数間の関係を表す式を「モデル式 」といいます.
例えば消費量 ~ 気温は変数「消費量」の変化を,変数「気温」を関連付けるという意味です.
この例の場合,変数「消費量」と「気温」という変数はbeerデータに含まれていますので,「data = beer」とデータ名を指定します.
> beer.lm <- lm (消費量 ~ 気温, data = beer) > summary(beer.lm) Call: lm(formula = 消費量 ~ 気温, data = beer) Residuals: Min 1Q Median 3Q Max -0.9764 -0.3472 0.1314 0.4178 0.6331 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.30710 0.36178 6.377 8.07e-05 *** 気温 0.19078 0.01917 9.953 1.66e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.5501 on 10 degrees of freedom Multiple R-squared: 0.9083, Adjusted R-squared: 0.8991 F-statistic: 99.06 on 1 and 10 DF, p-value: 1.659e-06
分析結果は保存して(ここでbeer.lmという名前で保存),summary()関数で要約を確認します.
結果は大きく4つのセクションにわかれます.
まずCall:は,この回帰式のモデル式です.
Residualsは,入力したデータの消費量と,回帰式が予測する結果との差(残差)を要約したものです.最小値,第1四分位数,中央値,第3四分位数,最大値の4つが出力されています.
Coefficients:は係数ですが,(Intercept) は切片を意味します.それぞれについて推定値(Estimate),その誤差(Std. Error),t値(t value),その確率(Pr(>|t|))の4つの数字が出力されています.
一番下には,この回帰分析の妥当性を表す決定係数 (Multiple R-squared),自由度調査済み決定係数 (Adjusted R-squared),F 統計量 (F-statistic) が表示されています. - 係数
分析結果から係数だけを取り出すことができます.
> (coefs <- coef(beer.lm)) (Intercept) 気温 2.307105 0.190785
(Intercept) というのが切片のことです.
- 予測値
回帰分析の推定した係数を使った予測値を求めます.predict()関数を使います.
> predict(beer.lm) 1 2 3 4 5 6 3.356422 3.566286 3.852463 5.321507 6.027412 6.580688 7 8 9 10 11 12 7.706320 7.820791 7.610927 5.779391 4.920859 3.966934 > data.frame(実際 = beer$消費量, 予測 = predict(beer.lm)) 実際 予測 1 2.38 3.356422 2 3.85 3.566286 3 4.41 3.852463 4 5.67 5.321507 5 5.44 6.027412 6 6.03 6.580688 7 8.15 7.706320 8 8.23 7.820791 9 7.35 7.610927 10 5.50 5.779391 11 4.90 4.920859 12 4.60 3.966934最初に予測値だけを表示しましたが,続いてdata.frame()関数を使って,実際の消費量と並べてみました.
