第6章 ロジスティック
最終更新日 2013 09 28
- ロジスティック回帰分析
- 二値変数
ロジスティック回帰分析とは,二値変数を目的変数とする回帰分析です. 二値変数とはYES/NO,あるいは 1 か 0 など,2つの選択肢のどちらかをとる変数です.
例としてタイタニック号のデータを取りあげましょう.RでTitanicと入力してEnterキーを押すと,表示されるデータがあります.これは豪華客船タイタニック号が沈没した際の乗客および乗務員の生存数を,性別,年齢,等級ごとに記録したデータです.
> Titanic , , Age = Child, Survived = No Sex Class Male Female 1st 0 0 2nd 0 0 3rd 35 17 Crew 0 0 , , Age = Adult, Survived = No Sex Class Male Female 1st 118 4 2nd 154 13 3rd 387 89 Crew 670 3 , , Age = Child, Survived = Yes Sex Class Male Female 1st 5 1 2nd 11 13 3rd 13 14 Crew 0 0 , , Age = Adult, Survived = Yes Sex Class Male Female 1st 57 140 2nd 14 80 3rd 75 76 Crew 192 20
生存できたか否かに,性別,年齢,等級が影響しているかどうかを,ロジスティック回帰分析で調べてみます.ここではRに保存されたデータ形式を少し変えてみたいと思います.
変換用の関数を備えているパッケージ(拡張ソフト)をRに追加します.次のコマンドを実行して下さい.
> install.packages("epitools")
フリーで公開されているRのパッケージサイトCRANから,丸括弧内に引用符で指定されたパッケージ(拡張ソフト)をダウンロードしてインストールします.
なお,この操作はRのウィンドウ上部のメニュー「パッケージ」「パッケージのインストール」「CRAN Mirrorの選択(Japan(Tokyo)など)」「Packages(の選択)」と,マウスで操作しても構いません.
インストール後,次のように操作してTitanicデータを変換します.変換できたかどうかをhead()関数で確認します.
> library(epitools) > > Titanic1 <- expand.table(Titanic) > head (Titanic1) Class Sex Age Survived 1 1st Male Child Yes 2 1st Male Child Yes 3 1st Male Child Yes 4 1st Male Child Yes 5 1st Male Child Yes 6 1st Male Adult No > nrow (Titanic1) [1] 2201
行ごとに,個別の乗客について,等級,性別,年齢(子供か大人か),そして生存したかを記録したデータになります.全部で2201行あります(nrow()関数でチェックします).これを集計したのが,オリジナルの Titanic データです.
生き残ったかどうか(YesかNoか)を目的変数として,等級,性別,年齢で説明してみます.
回帰分析では lm() という関数を使いましたが,ロジスティック回帰分析では glm() という関数を使います.
丸括弧内には,おなじみのモデル式 「Survived ~ +Sex + Age+ Class」と,データの名前「data = Titanic1」,そしてロジスティック回帰分析を実行することを意味する「family = "binomial"」の3つの引数を,コンマで区切って並べます.
分析結果を,適当な名前で保存し,これにsummary()関数を適用して結果を確認するのは同じです.
> Titanic.glm <- glm(Survived ~ +Sex + Age+ Class, data = Titanic1, family = "binomial") > summary (Titanic.glm) Call: glm(formula = Survived ~ Sex + Age + Class, family = "binomial", data = Titanic1) Deviance Residuals: Min 1Q Median 3Q Max -2.0812 -0.7149 -0.6656 0.6858 2.1278 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 0.6853 0.2730 2.510 0.0121 * SexFemale 2.4201 0.1404 17.236 < 2e-16 *** AgeAdult -1.0615 0.2440 -4.350 1.36e-05 *** Class2nd -1.0181 0.1960 -5.194 2.05e-07 *** Class3rd -1.7778 0.1716 -10.362 < 2e-16 *** ClassCrew -0.8577 0.1573 -5.451 5.00e-08 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 2769.5 on 2200 degrees of freedom Residual deviance: 2210.1 on 2195 degrees of freedom AIC: 2222.1 Number of Fisher Scoring iterations: 4
注目するのは,やはりCoefficientsのところです.
まず(Intercept) ですが,これは切片です.より具体的にいうと,性別が男性,年齢が子供,等級が1等客室の乗客の場合の推定値です.
実際にこの条件で予測をおこなってみると以下のようになります.
> newData <- data.frame (Sex = "Male", Age = "Child", Class = "1st" ) > predict(Titanic.glm, newdata = newData) 1 0.6853195 > predict(Titanic.glm, newdata = newData, type = "response") 1 0.6649249
最初にnewDataという名前で,性別が男性,年齢が子供,等級が1等客室の乗客というデータを作っています.predict関数に,先のロジスティック回帰分析の結果と,いまの新規データを指定して実行してみると,予測値が出ます.
predict()関数を二度実行していますが,最初の出力は,先ほどの切片(Intercept)と同じ0.6853ですが,これは対数オッズです.
二度目の実行では,「type = "response"」を追加しています.これは対数オッズを確率に変える指定です. 結果の 0.66,約 66% が生き残る確率になります.
Coefficients: の欄の切片の下は,まず女性の場合対数オッズで 2.4201 が追加されます.これは対数を外すと(exp(2.4201)を計算すると),約11で,女性の場合,生存率が 11 倍に跳ね上がることを意味します.
また年齢が成人(Adult)の係数は -1.0615 で負の値です.これは成人の場合,生存率が三分の1に減少することを意味します( exp (-1.06)を計算).
以下同様に,Class2ndは等級が2等の場合,class3rdは3等の場合,そしてClassCrewは乗務員を表しますが,いずれもマイナスなので,生存率は下がっていることになります.
- 決定木
- 決定木は,ある選択に影響を与えている要因を探る手法です.
先ほど作成したタイタニック号データを使って実例を示します.
Rで実行するには rpart という追加パッケージが必要ですが,本書の付録ソフトウェアで demo(startup) を一度でも実行している場合,お使いのRにはすでに追加インストールされています.
> library(rpart) > Titanics.rpart <- rpart (Survived ~ Sex + Age+ Class, data = Titanic1) > Titanics.rpart n= 2201 node), split, n, loss, yval, (yprob) * denotes terminal node 1) root 2201 711 No (0.6769650 0.3230350) 2) Sex=Male 1731 367 No (0.7879838 0.2120162) 4) Age=Adult 1667 338 No (0.7972406 0.2027594) * 5) Age=Child 64 29 No (0.5468750 0.4531250) 10) Class=3rd 48 13 No (0.7291667 0.2708333) * 11) Class=1st,2nd 16 0 Yes (0.0000000 1.0000000) * 3) Sex=Female 470 126 Yes (0.2680851 0.7319149) 6) Class=3rd 196 90 No (0.5408163 0.4591837) * 7) Class=1st,2nd,Crew 274 20 Yes (0.0729927 0.9270073) *
Titanics.rpart <- rpart (Survived ~ Sex + Age+ Class, data = Titanic1)の部分が,生存か否かに影響のあった変数として,性別,年齢,等級を検討してみることを表す命令です.
結果も表示しましたが,これはグラフ化したほうが分かりやすいです.ここでは,決定木を見やすくするパッケージ rpart.plot を使ってグラフ化した結果を表示します.必要な追加パッケージは,やはり demo(startup) を実行していれば導入済みです.
> library(rpart.plot) > prp(Titanic.rpart, type=2, extra=101, nn=TRUE, fallen.leaves=TRUE, faclen=0, varlen=0, shadow.col="grey", branch.lty=3, cex = 1.2, split.cex=1.2, under.cex = 1.2)
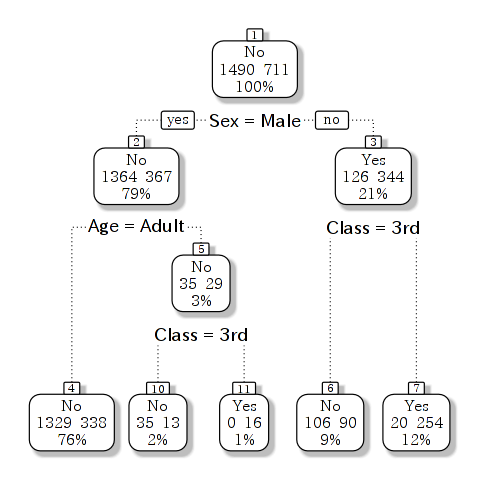
画像を生成するprp()関数の中身が複雑ですが,主に文字のサイズなどの指定です.
図で最上部に「No 1490 711」とあるのは,データ全体で死亡が 1490 名,生存者が 711 名という意味です.
箱の下に「Sex=Male」とあり,性別が男性なら左下のコースに,女性なら右下のコースに進みます.右下に進むと女性のうち 344 名が生存(Yes),126名が死亡したことが分かります.
この下の条件は「Class=3rd」とあって,等級が3等客室であれば左,1,2当客室であれば右におります.3等客室の場合死亡者のほうが 106 名と多いことが分かりますが,1,2 等客室の場合は生存者のほうがはるかに多く 254 名と分かります.
また最上部に戻って,「Sex=Male」がYesの場合には1364名が No, つまり死亡していますが,その下の「Age=Adult」がNoの場合,つまりは子供の場合,右下に進みます.この場合35名が死亡していますが,その下に内訳があり,「Class=3rd」がNoのとき,つまり1,2等客室の場合は 16名全員が救出され生き残ってます.
決定木は,大規模データ(この場合は 2201 程度ですが)を対象に,ある選択に影響を与えている要因を検証するのに優れた手法です.
- 独立性の検定(カイ自乗検定)
- 分割表の検定
たとえば,西洋人で眼の色と髪の色には対応があるような気がしませんか?
Rには HairEyeColor というデータがありますが,この一部が以下のようになっています.
> HairEyeColor[ ,, Sex = "Female"] Eye Hair Brown Blue Hazel Green Black 36 9 5 2 Brown 66 34 29 14 Red 16 7 7 7 Blond 4 64 5 8
これはアメリカのある大学で,統計学の受講者を調査した結果から,女性のデータだけ取り出したデータです.また,このような度数(頻度)表を 分割表ともいいます.
行(右側)に髪 (Hair)の色の種類が,列(上)に眼(Eye)の色の種類があります.
たとえば髪が黒(Black)の場合,目は茶色(Brown)系統が 36 名と圧倒的に多いのですが,髪がブロンド(Blond)の女性だと,64名が目はブルー(Blue)だということが分かります.
どうやら髪がダーク系統だと眼の色は茶色が多く,ブロンドでは目は青に偏っているようです.
これが,このクラスが偶然そうであったのか,あるいは西洋人の場合,一般的に目と髪のそれぞれの色には対応があるのかを,確率的に検討するのが,「仮説検定」です.
仮説には2種類あり,
- 帰無仮説:髪の色と眼の色は独立である(互いに関係ない)
- 対立仮説:髪の色と眼の色は独立ではない(互いに関係がある)
統計的検定では,帰無仮説をたてて検定を行い,出力されたP値が0.05より小さい場合,帰無仮説を捨てて,対立仮説を採用するという手順をとります.
この場合は独立性の検定 (あるいはカイ自乗検定 ともいいます)を適用します.
Rでは chisq.test()という関数に引数としてデータを指定するだけです.
> chisq.test (HairEyeColor[ ,, Sex = "Female"]) Pearson's Chi-squared test data: HairEyeColor[, , Sex = "Female"] X-squared = 106.6637, df = 9, p-value < 2.2e-16 警告メッセージ: In chisq.test(HairEyeColor[, , Sex = "Female"]) : カイ自乗近似は不正確かもしれません出力で重要なのは「X-squared」カイ自乗値,「df」自由度,そして「p-value」P値です.
P値が 0.05 未満であれば,帰無仮説を棄却して対立仮説を採択します.
つまり,髪の毛と眼の色には関連性があると結論づけられます.
なお,このデータには,頻度が 2 や 4 という比較的小さな値が含まれているため,「カイ自乗近似は不正確かもしれません」という警告が出力されています.
- 分割表の作成
-
データフレームから分割表を作成するには xtabs() という関数を使います.
元のデータフレームの名前を「表1」として,ここから弁当と時間を基準に,購入した人数を集計するには xtabs()関数を次のように使います.
> head (表1) 弁当 性別 年齢 時間 1 果 女 20 晩 3 野 女 30 昼 4 果 女 20 晩 5 果 女 30 晩 7 果 女 20 昼 8 野 女 30 昼 > xtabs(~ 弁当 + 時間, data = 表1) 時間 弁当 昼 晩 果 4 10 野 9 2xtabs()関数に引数として指定している「~ 弁当 + 時間」は行に「弁当」を,また列に「時間」をとって集計するという意味です.ただし「data = 表1」でデータを指定する必要があります. - 行列の作成
2行2列程度の分割表であれば,Rで行列という形式で作成するのが手軽です. matrix() という関数を使います.
> dat <- matrix (c( 4, 10, 9, 2), nrow = 2) > dat [,1] [,2] [1,] 4 9 [2,] 10 2「matrix」に続く丸括弧内にカンマを挟んで数値を指定します.ここではc()関数内に4つの数値を並べています.「ncol=2」は 2 列の行列を作成するよう指定してます.行数は自動的に判断されます.
簡単のため行と列のラベルを指定しなかったので,単に行数と列数を表す「[1,] 」などが分割表の左と上に表示されています.
ここでは分析結果を「dat.test」という名前で保存しました.それは分析の途中経過などの情報を確認できるからです.
> dat.test$observed [,1] [,2] [1,] 4 9 [2,] 10 2 > dat.test$expected [,1] [,2] [1,] 7.28 5.72 [2,] 6.72 5.28 > dat.test$observed - dat.test$expected [,1] [,2] [1,] -3.28 3.28 [2,] 3.28 -3.28「dat.test」の後ろに「$」をつけ,さらに「observed 」を入力してEnterキーを押すと観測値,つまり元のデータが表示されます.「$」に「expected」を続けると,期待値です.したがって,2つを引き算すれば,実際のデータと理論的な値との差を求めることができます.
「$」に「statistic」を続けて入力してEnterキーを押すと,カイ自乗値が表示されます.
> dat.test$statistic X-squared 5.026484 > dat.test Pearson's Chi-squared test with Yates' continuity correction data: dat X-squared = 5.0265, df = 1, p-value = 0.02496
ただし,この数値は,本書に掲載した数値と異なっています.
それはchisq.test()関数がデフォルトでは「イェーツの補正 」を行うからです.すなわち元データと期待値の差に補正のための数値を足し算しているのです.
本書に示した計算結果と同じ数値を出力させるには,chisq.test()関数にイェーツの補正を行わないよう「correct = FALSE」を追加して実行します.
> chisq.test (dat, correct = FALSE) Pearson's Chi-squared test data: dat X-squared = 6.9972, df = 1, p-value = 0.008164
